Persistent / Immutable Treaps

Prerequisites: Should have a good understanding of Treaps (both Vanilla / BST and Implicit), along with some basic understanding of BSTs and Segment Trees. I had given a presentation at work which can serve as a good starting point. You can also refer to the following tutorials: Vanilla Treaps as BST, Implicit Treaps, or the original research paper.

If you are familiar with Treaps in Competitive Programming context, you’d know that there are two main operations that a Treap fundamentally supports— split and merge.

The split operation takes a given treap and a value (say k), and breaks the given treap into two treaps, one with values ≤ k and the other with values > k.

Similarly, the merge operation takes two treaps, say L and R, such that all values in L are ≤ all values in R, and merges them to create a new Treap T.

Both these operations work in O(log(N)) (assuming N is the size of the treap before split or after merge). As you might guess, irrespective of the provided value for splitting the treap or the skew in the size of the treaps before merging, only O(log(N)) nodes are modified in total.

What if instead of modifying those O(log(N)) nodes, we created new nodes every time a modification is necesssary? That’d give us the following:

We’d have every “version” of the tree. A version of the treap is created every time you call split or merge.
You get some thread-safety for free. If it’s okay to have multiple versions of the treap, then no locking/waiting is required.
If you merge two implicit treaps, then you have access to 3 implicit treaps (the 2 original and the merged one) with only O(log(N)) extra memory.

The first and last property above are sometimes used in hard contest problems. However, before going to the problems, let’s see how persistent treaps work and look like:

How Persistent Treaps Work

Let’s consider the case for Implicit Persistent Treaps with the following arrays:

Implicit Treaps don't store the BST values explicitly and instead infer them from the subtree sizes. These are used for doing operations on arrays, and allow you to perform pretty mind-boggling stuff in O(log(N)) time, like reversing a sub-array, transplanting a sub-array within the array, etc. while still supporting range aggregate queries like sum, min, etc. in O(log(N)).

A = [1, 10, 3, 2, 1]

B = [2, 2, 2, 3, 4]

The array we get after merging A and B will be:

AB = [1, 10, 3, 2, 1, 2, 2, 2, 3, 4]

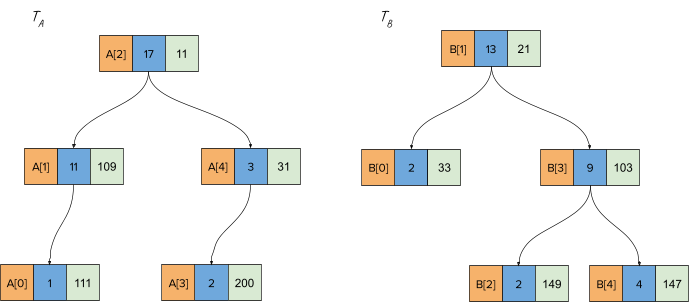
Let’s say the corresponding treaps for the above arrays are called T_A, T_B, T_AB. Moreover, assume the aggregate function we have to maintain is simply sum to answer range sum queries over the arrays.

Persistent Treap Merge Operation

Let’s walk through a merge operation call for the treaps T_A and T_B to generate T_AB

The nodes in the following diagrams represent the following:

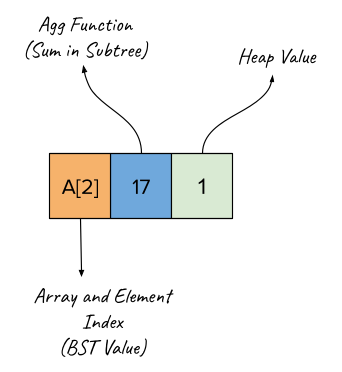
Let’s say treaps T_A and T_B look as follows. Note that the heap values are generated randomly, and hence we can get a different treap for a given array every time. Also, the treaps in this tutorial are min-heap ordered.

Now if we call merge for the treaps T_A and T_B, the first merge call will pick the node corresponding to A[2] since that one has a lower heap value (11). Moreover, as is the case usually with merge operations , if we pick the treap on the left (T_A), we will keep it’s left-child as is and call merge with the left treap’s right child (A[4]) and the full treap on the right (T_B or B[1]). This looks as follows:

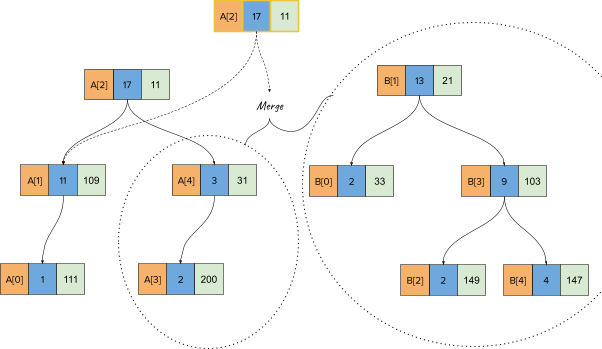
Now, we will pick the node corresponding to B[1] since that one has a lower heap key (21), keeping its right child as is and calling merge with its left-child. This looks as follows:

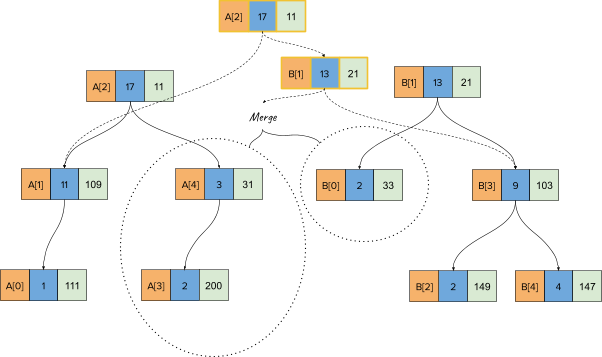
Finally, we pick the node corresponding to A[4] and take its left child as is, and call merge with the node corresponding to B[0] and A[4]’s right-child, which is NULL. That will yield the following treap structure (before recursion has returned):

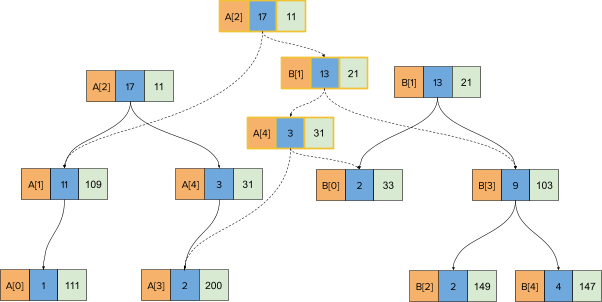
When the recursion stack returns, the aggregate functions will be corrected for the nodes to yield this final state:

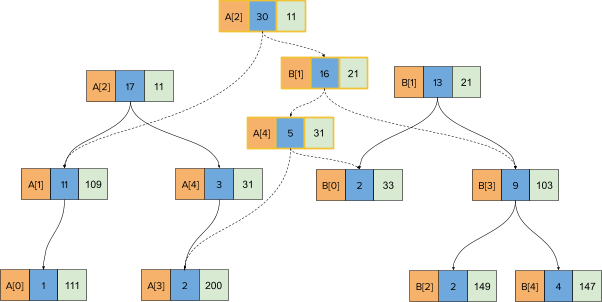
Note that the number of new nodes created is O(height(T_A) + height(T_B)) which is O(log(N)) with a fairly high probability.

As you can see in the last image above, even after merging the original two treaps, you have complete access to both the original treaps as well as the merged treap. Also note that none of the original treap nodes are modified (immutability).

Persistent Treap Split Operation

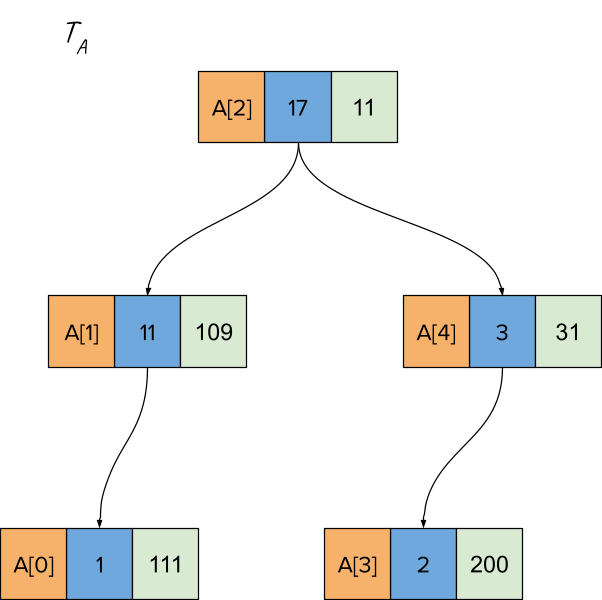
Let’s also walk through a split operation for the treap T_A. Let’s say the key for splitting is 3, meaning we should break the treap into two treaps, one with array elements with indices <= 3 and the other with indices > 3. Since A had five elements, the treap on the left should have 4 elements and the treap on the right should have a single element.

This is how treap T_A initially looks:

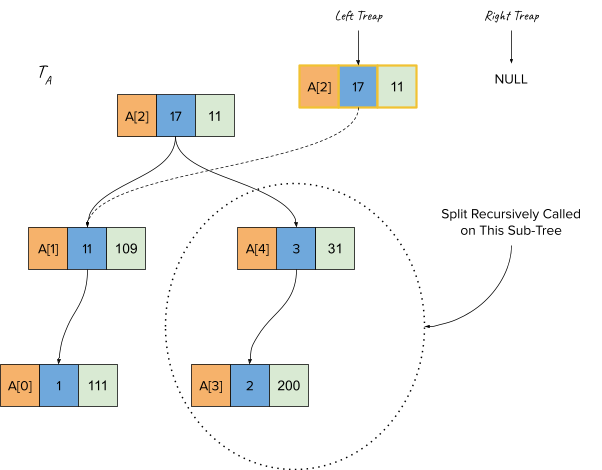
In the first call for split, since the node A[2]’s BST Value (array index, i.e. 2) is less than the splitting key (which is 3), we create a new node and make this the root of the left treap. The recursive call for split is made for the sub-treap rooted at A[4] (as shown below).

Reminder: In regular treaps (non-persistent), when we call split and the current node's value is <= the splitting key, we assign that node to the left output treap of the split call, keeping the left sub-treap / child of the current node as is, and call split recursively on the right sub-treap. Similarly, if the value of the current node is greater than the splitting key, we assign that node to the right output treap of the split call, keeping the right sub-treap / child of the current node as is, and call split recursively on the right sub-treap.

Now, the split operation is called for node A[4], and since that has a higher BST Value (4) than the splitting key (3), we make this the root of the right treap and call split on the left sub-treap of A[4] (i.e. A[3])

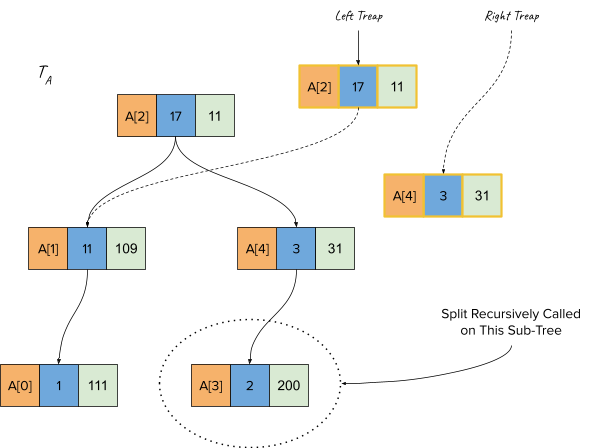
Finally, the split call reaches A[3] and since its value is <= splitting key, we make this the right child of the left treap.

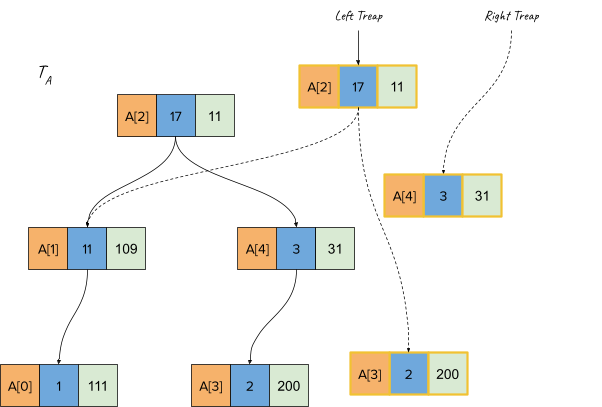
Finally, when the recursion stack returns and the aggregate function (sum) is recomputed, we get the following final treap:

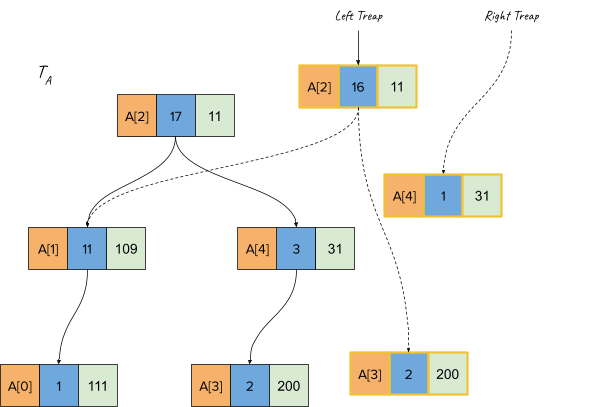
Sample Problems

Problem-1: Codechef August 2010 Challenge / Problem: GENETICS

You are given a bunch of DNA sequences (in a list called L), and you have to support the following operations:

CROSS id1 id2 k1 k2: Create two new DNAs from DNA[id1] and DNA[id2] and add them to L: L.append(L[id1][:k1] + L[id2][k2+1:]) and L.append(L[id2][:k2] + L[id1][k1+1:])
MUTATE id1 k X: Set the base at index k for DNA L[id1] to X (X will be either of ‘A’, ‘G’, ‘C’, ‘T’)
COUNT id1 k1 k2: Return number of each of the 4 bases in DNA L[id1] between indices k1 and k2.

Solution:

This is a direct application of persistent treaps. The aggregate function will need to track sum for each of the 4 bases (AGCT). You can find my Accepted implementation here: Gist on GitHub

You can see the split and merge methods below, which create a new node for every visited node:

This question also requires you to support point updates (setting a given element to a given value). This can also be done by keeping the treaps immutable. Refer to the point_update method in the implementation.

One important caveat for my linked solution (and even other implementations for this problem) is that there are some memory leaks (Can you figure out where?). However, the memory limit is high enough that it doesn’t become an issue.

Problem-2: Problem C from Day-4 of Summer Petrozavodsk Camp (statements)

You are given an array with N (<= 2e5 elements) and you have to support the following 3 operations:

SUM L R: Return the sum of all elements between indices L and R (both inclusive).
REP L R K: Modify the array as per the following pseudocode: for (int i = l; i <= r; i++) A[i] = A[i - k];
REVERT L R: Change all elements in indices L and R to their original value.

This is a custom-built theme for Jekyll. Please report any issues on GitHub.